안녕하세요, 여행벌입니다.
오늘은 그래프 탐색 기법 중 너비 우선 탐색(BFS)에 대해서 포스팅해보겠습니다.
그래프(graph)
그래프(graph)는 연결되어 있는 객체 간의 관계를 표현할 수 있는 자료 구조입니다. 수학자 오일러에 의해 처음 창안되었으며, 정점(vertex)와 간선(edge)로 그래프를 표현합니다. 정점은 노드(node)라고도 불리며, 간선은 링크(link) 라고도 불립니다. 아래 그림과 같이 지도를 나타낼 때 그래프가 많이 이용됩니다.

너비 우선 탐색(BFS)
너비 우선 탐색은 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법입니다. 너비 우선 탐색을 위해서는 방문한 정점들을 차례로 저장한 후 꺼낼 수 있는 자료 구조 큐(queue)가 필요하고, 방문한 정점들을 체크하는 bool 배열이 필요합니다.
예시를 통해서 BFS 탐색 순서를 익혀보겠습니다.
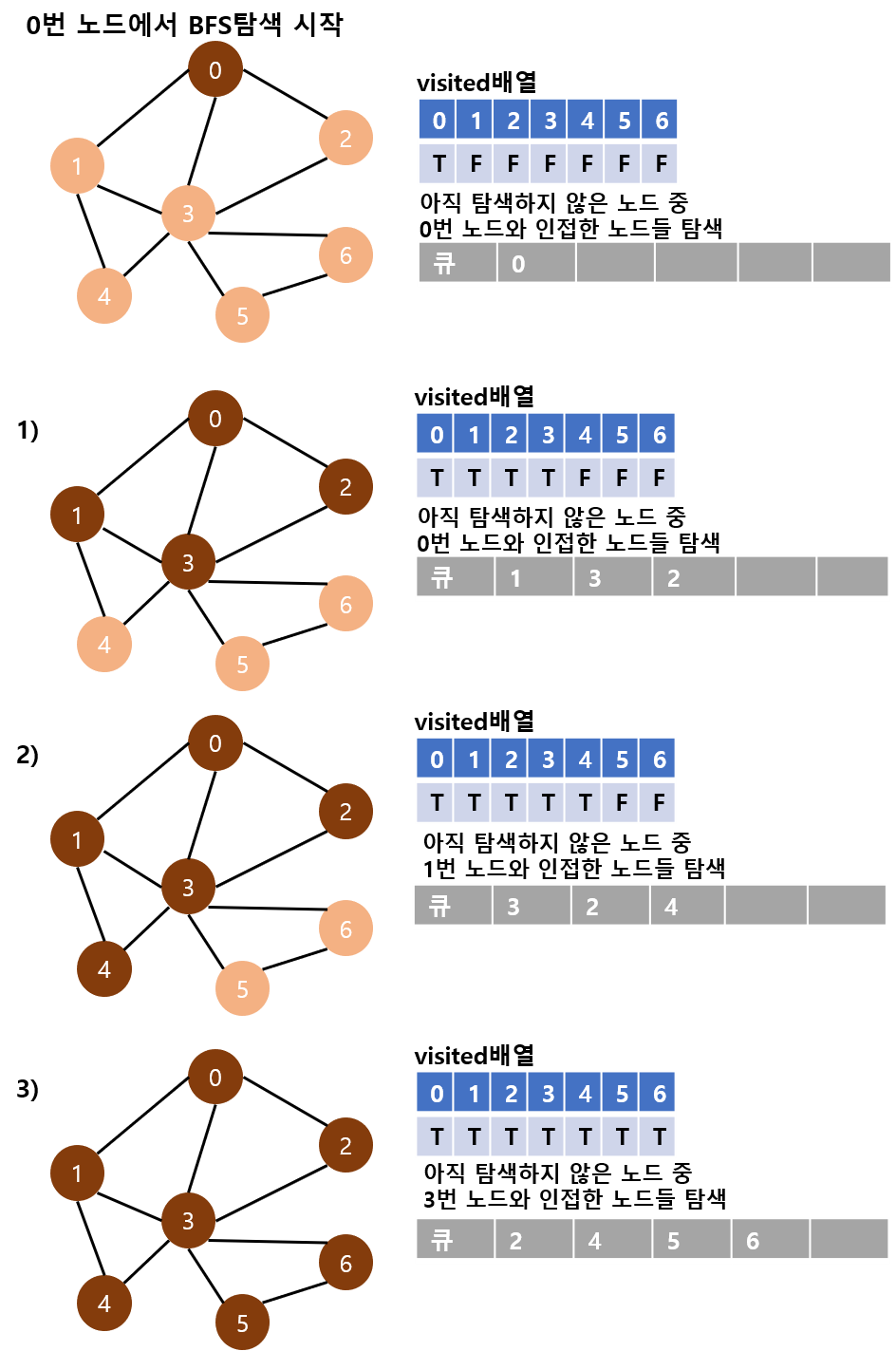

BFS 탐색은 다음과 같은 순서로 진행됩니다.
1) 큐의 가장 앞에 있는 노드(현재 방문 중인 노드)와 연결된 노드 중, 방문하지 않은 노드가 있다면 큐에 삽입하고 방문 표시를 한다.
2) 1)의 과정을 큐에 더 이상 노드가 없을 때까지 반복한다.
코드 구현 ( C )
인접 행렬로 표현된 그래프에 대한 BFS
void bfs_mat(GraphType* g, int v) {
QueueType q;
init(&q);
visited[v] = TRUE; // v정점에서부터 탐색 시장
enqueue(&q, v);
while (!is_empty(&q)) { // 큐에 남은 정점이 없을 때까지 진행
v = dequeue(&q);
printf("%d 정점을 방문\n", v);
for (int w = 0; w < g->n; w++) {
if (g->adj_mat[v][w] && !visited[w]) { // 간선이 존재하고 방문하지 않은 정점
visited[w] = TRUE;
enqueue(&q, w);
}
}
}
}인접 리스트로 표현된 그래프에 대한 BFS
void bfs_list(GraphType* g, int v) {
GraphNode* w;
QueueType q;
init(&q);
visited[v] = TRUE;
enqueue(&q, v);
while (!is_empty(&q)) {
v = dequeue(&q);
printf("%d 정점을 방문\n", v);
for (w = g->adj_list[v]; w; w = w->link) {
if (!visited[w->vertex]) {
visited[w->vertex] = TRUE;
enqueue(&q, w->vertex);
}
}
}
}코드 구현 ( C++ )
인접 행렬로 표현된 그래프에 대한 BFS
void bfs_mat(int v) { // 정점의 수 N개 graph[x][y] 는 x에서 y로 가는 간선을 의미.
queue<int> q;
bool visited[N] = {};
q.push(v);
visited[v] = 1;
while (!q.empty()) {
int cur = q.front();
cout << cur << "노드를 방문 중\n";
q.pop();
for(int i = 0; i < N; i++)
if (graph[cur][i] && !visited[i]) {
visited[i] = true;
q.push(i);
}
}
}벡터로 표현된 그래프에 대한 BFS
void bfs_mat(int v) { // 정점의 수 N개 graph[x][y] 는 x에서 y로 가는 간선을 의미.
queue<int> q;
bool visited[N] = {};
q.push(v);
visited[v] = 1;
while (!q.empty()) {
int cur = q.front();
cout << cur << "노드를 방문 중\n";
q.pop();
for(int i = 0; i < graph[cur].size() ; i++)
if (graph[cur][i] && !visited[i]) {
visited[i] = true;
q.push(i);
}
}
}너비 우선 탐색의 복잡도
● 인접 행렬로 표현된 경우 N개의 노드에 대해서 N 개의 다른 노드와 연결되어있고, 방문되지 않은 노드를 체크해야되므로 O(N^2)의 시간 복잡도를 가집니다.
● 자료구조 vector 혹은 연결 리스트로 표현된 경우 N개의 노드에 대해서 연결된 M개의 간선만큼만 탐색을 진행하므로 O(N + M)의 시간 복잡도를 가집니다.
이상으로 유명한 그래프 탐색 방법 중 하나 인 너비 우선 탐색(BFS) 포스팅을 마치겠습니다.
'Computer Science > Algorithm' 카테고리의 다른 글
| [알고리즘] 트라이(Trie) 란 (0) | 2020.04.23 |
|---|---|
| [알고리즘] 깊이 우선 탐색(DFS)이란 (0) | 2020.04.06 |
| [알고리즘] 서로소 집합(Disjoint set) & 유니온-파인드 (Union-Find) 란 (1) | 2020.04.01 |
| [알고리즘] 합병 정렬(Merge sort) 란 - travelbeeee (0) | 2020.01.15 |
| [알고리즘] 퀵 정렬(quick sort) 란 - travelbeeee (0) | 2020.01.14 |