굳건하게

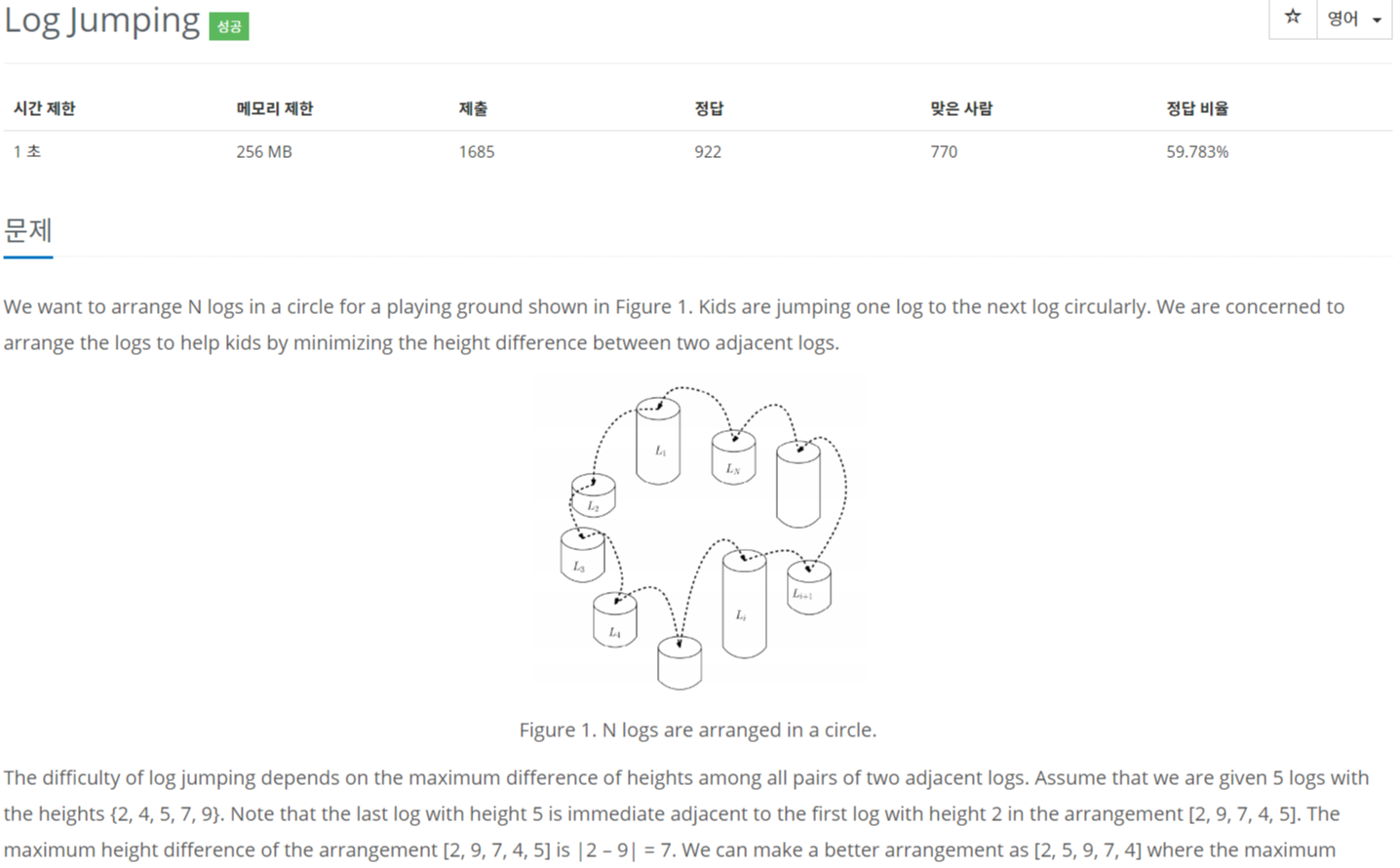
안녕하세요.

여행벌입니다.

오늘은 ACM-ICPC 2015 본선 문제인

BOJ 11501 Stock 문제풀이를 해보겠습니다.

[문제해석]

당신은 주식을 1개 사거나, 그동안 사온 주식을 팔거나, 아무것도 안 하거나 3가지 일 중 하나만 하루에 행동할 수 있다. 이때, N일 동안의 주식 가격이 주어졌을 때, 얻을 수 있는 최대 이익을 구하는 알고리즘을 구현하라.

Ex)

[ 1 1 3 5 4 2 3 ] 7일 동안 주식 가격이 주어졌다고 가정해보자.

1일 차, 2일 차, 3일 차는 4일 차인 주식 가격이 최대치인 5일 때 팔아야 되고,

6일 차는 7일 차인 주식 가격이 3일 때 팔아야 된다.

즉, i 일차 주식이 얻을 수 있는 최대 이익은 (i + 1) ~ 마지막 날까지 중 가장 주식 가격이 큰 날 팔아야 된다.

[쓴이생각]

문제는 생각보다 간단하지만, 알고리즘을 생각해내기까지 굉장히 오래 걸렸다.

처음 든 생각은 '무식하게 구해보자.'였다.

앞에서부터 순회하며 각각의 날에 대해 최대 이익을 구했다.

i 번 째 날의 최대 이익을 구하기 위해, (i + 1 ) ~ 마지막 날까지 순회하며 Max를 구해 최대 이익을 구했다.

당연히, O(n^2) 으로 시간 초과를 했다.

그다음 생각은 '뒤에서부터 순회를 해보자.'였다.

뒤에서부터 순회하면 Max를 구하기 위해 따로 순회할 필요가 없다.

예를 들어, [5 7 9 11] 이라고 해보자. 9 입장에서는 뒤에서부터 찾아온 11이라는 Max값이 중요하고, 5, 7 입장에서도 뒤에서부터 가져온 11이라는 Max 값이 중요하다.

즉 뒤에서부터 순회하면, Max 값을 그냥 순회할 때, If 문 하나로 계속 찾아줄 수 있다.

[알고리즘설계]

뒤부터 순회하며 Max는 마지막 날의 이익부터 시작해서 더 큰 이익을 저장해나가며 갱신한다.
Result에는 i번 째 날의 주식 값보다 Max가 더 크다면 Max - dp_list[i] 를 더해가며 쌓는다.

다음과 같이 예시를 통해 생각해보자.
index      0  1  2  3 4 5 6 7 8 9 10
Number    1  4  10 8 7 4 7 5 2 3 1
Max         10 10 10 8 7 7 7 5 3 3 1
Result      19 10 4  4 4 4 1 1 1 0 0 

#include<cstdio>

using namespace std;

int nlist[1000000];

int main(void) {
	int test_case;
	scanf("%d", &test_case);
	for (int i = 0; i < test_case; i++) {
		int ninput;
		scanf("%d", &ninput);
		for (int j = 0; j < ninput; j++) {
			scanf("%d", &nlist[j]);
		}
		int max = 0;
		long long result = 0;
		for (int j = ninput - 1; j >= 0; j--) {
			if (max < nlist[j])
				max = nlist[j];
			if (max > nlist[j])
				result += max - nlist[j];
		}
		printf("%lld\n", result);
	}
}

아이디어를 떠올리기까지 오래 걸렸지만, 좋은 아이디어를 생각해내서 깔끔하게 풀 수 있었다.

안녕하세요.

여행벌입니다.

오늘은 ACM-ICPC 2016 본선 문제인

BOJ 13560번 Football Game 문제풀이를 해보겠습니다.

[문제해석]

N개의 축구팀이 서로 다른 모든 팀과 한 번씩 축구시합을 진행한다. 이때, 이기면 +1점 지면 0점을 얻는다.

이 때, N개의 팀에 대한 승점 리스트가 주어졌을 때, 유효한 리스트면 "1", 아니면 "-1"을 출력하는 알고리즘을 구현하라.

[필요한지식]

-Tournament Graph 개념

N개의 팀이 있을 때, 각각의 팀을 노드로 생각하고,

A가 B를 이기면, A에서 B로 가는 방향을 가진 Edge를 추가해 Graph를 만든다고 생각해보자.

A에서 B로 가는 Edge가 있다면, B에서 A로가는 Edge는 존재하지 않을 것이고, N개의 노드가 있을 때, n(n-1)/2 개의 Edge가 생길 것이다. 이런 Graph를 Tournament Graph라고 부른다.

-Landau's Theorem

Graph의 노드에 대한 Degree를 오름차순으로 (S1, S2, ⋯ Sn) 으로 정렬했을 때,

다음과 같은 두 성질을 만족한다면, Tournament Graph이다.

각 팀의 승점 리스트는 해당 노드의 Degree이므로, 우리는 주어진 승점 리스트로 Landau's Theorem을 이용해 Tournament Graph인지 아닌지 판단하면 된다.

#include<cstdio>
#include<algorithm>

int main(void) {
	int ninput, list[10000], sum = 0;
	scanf("%d", &ninput);
	for (int i = 0; i < ninput; i++) {
		scanf("%d", &list[i]);
	}
	std::sort(list, list + ninput);
	for (int i = 0; i < ninput; i++) {
		sum += list[i];
		if (sum < ((i + 1) * i) / 2) {
			printf("-1");
			return 0;
		}
	}
	if (sum == (ninput * (ninput - 1)) / 2)
		printf("1");
	else
		printf("-1");
	return 0;
}

Landau's Theorem을 몰라서 정말 헤매다가 해결한 문제다...

안녕하세요.

여행벌입니다.

오늘은 ACM-ICPC 2015 본선 문제인

BOJ 11497 Log Jumping 문제를 다뤄보겠습니다.

[문제해석]

N개의 통나무의 높이가 주어지고 우리는 이 통나무를 동그랗게 배치할 것이다.

이때, 통나무 사이의 높이 차이 중 가장 큰 값이 가장 작게 나올 때, 그 값을 출력하는 알고리즘을 구현하라.

예를 들어, 높이가 2,4,5,7,9 인 5개의 통나무를 가지고 [ 2 - 4 - 5 - 7 - 9 ]로 배치를 하면,

통나무 높이 차이 중 가장 큰 값은, 높이가 2인 통나무와 9인 통나무 사이의 높이 차인 7이 된다.

배치를 바꿔 [7 - 4 - 2 - 5 - 9 ] 로 배치를 하면, 통나무 높이 차이 중 가장 큰 값은 높이가 5인 통나무와 9인 통나무 사이의 높이 차인 4가 된다.

[알고리즘설계]

1. 통나무 높이가 주어지면 오름차순으로 sort를 진행한다.

2. n개의 통나무가 주어졌을 때, 높이가 작은 통나무부터 A1, A2, ⋯ , An 이라고 하자.

우리는 높이 차이를 최소화해야 하므로, 비슷한 통나무들끼리 배치해줘야 한다.

따라서 가장 작은 통나무부 A1을 배치하고, 그다음에는 A2, A1, A3 식으로 주변에 배치를 진행할 것이다.

->  ⋯ A4, A2, A1, A3, A5  ⋯ 형태로 배치한다.

3. 실제로 배치할 필요는 없으므로, 2번의 아이디어를 통해 A1부터 시작해 양 옆에 올 통나무들과의 거리 차를 계속 계산해나가며, 그중 MAX를 저장한다.

#include<iostream>
#include<algorithm>

using namespace std;

int list[10000];

int main(void) {
	int test_Case;
	cin >> test_Case;
	for (int i = 0; i < test_Case; i++) {
		int ninput;
		cin >> ninput;
		for (int j = 0; j < ninput; j++)
			cin >> list[j];
		sort(list, list + ninput);

		int distance = list[2] - list[0];

		if (ninput % 2 == 1) {
			for (int j = 1; j <= ninput - 4; j += 2) {
				if (list[j + 2] - list[j] > distance)
					distance = list[j + 2] - list[j];
				if (list[j + 3] - list[j + 1] > distance)
					distance = list[j + 3] - list[j + 1];
			}
		}
		else {
			for (int j = 1; j <= ninput - 5; j += 2) {
				if (list[j + 2] - list[j] > distance)
					distance = list[j + 2] - list[j];
				if (list[j + 3] - list[j + 1] > distance)
					distance = list[j + 3] - list[j + 1];
			}
			if (list[ninput - 1] - list[ninput - 3] > distance)
				distance = list[ninput - 1] - list[ninput - 3];
		}
		if (i != test_Case - 1)
			cout << distance << "\n";
		else
			cout << distance;
	}
}

Indexing이 까다로워서 실수가 있었지만, 그래도 ACM-ICPC 문제 치고는 쉬운 편인 것 같습니다.

안녕하세요

여행벌입니다.

오늘은 ACM-ICPC 2015 본선 문제인

BOJ 11592번 3-Primes Problem 문제를 다뤄보도록 하겠습니다.

[문제해석]

7 ~ 1000 사이의 양수가 주어졌을 때, 이 양수를 3개의 소수의 합으로 표현할 수 있다면, 3개의 소수를 출력하고, 아니라면 0을 출력하는 알고리즘을 작성하여라.

[알고리즘설계]

1. 에라토스테네스 체를 이용하여 1 ~ 1000 사이의 소수를 먼저 찾는다.

2. 3중 포문을 이용해 주어진 양수(ninput)를 3개의 소수의 합으로 판단할 수 있는지 없는지 판단한다.

* Input 값의 범위가 1000 으로 매우 작다. 따라서, 무식하게 3중 포문을 이용해서 푸는 것이 빠르겠다고 판단하였다.

#include<iostream>

using namespace std;

int main(void) {
	// 에라토스테네스체로 prime부터 찾자.
	bool prime[1001];
	for (int i = 0; i < 1001; i++)
		prime[i] = true;
	for (int i = 2; i * i <= 1000; i++) {
		if (prime[i] == true) {
			for (int j = 2 * i; j <= 1000; j += i) {
				prime[j] = false;
			}
		}
	}

	int test_case;
	cin >> test_case;
	for (int i = 0; i < test_case; i++) {
		int ninput, j , k , l;
		cin >> ninput;
		for (j = 2; j < 1000; j++) {
			for ( k = 2; k < 1000; k++) {
				for ( l = 2; l < 1000; l++) {
					if (j + k + l > ninput)
						break;
					if (prime[j] && prime[k] && prime[l] && j + k + l == ninput){
						cout << j << ' ' << k << ' ' << l << '\n';
						break;
					}
				}
				if (prime[j] && prime[k] && prime[l] && j + k + l == ninput) {
					break;
				}
			}
			if (prime[j] && prime[k] && prime[l] && j + k + l == ninput) {
				break;
			}
		}
		if (prime[j] && prime[k] && prime[l] && j + k + l == ninput) {
			continue;
		}
		else
			cout << 0 << '\n';
	}
	return 0;
}

input이 작아서 문제에 쉽게 접근할 수 있었지만, input이 크다면 접근하기 어려울 것 같다.