
안녕하세요.
여행벌입니다.
오늘은 ACM-ICPC 2015 본선 문제인
BOJ 11497 Log Jumping 문제를 다뤄보겠습니다.

[문제해석]
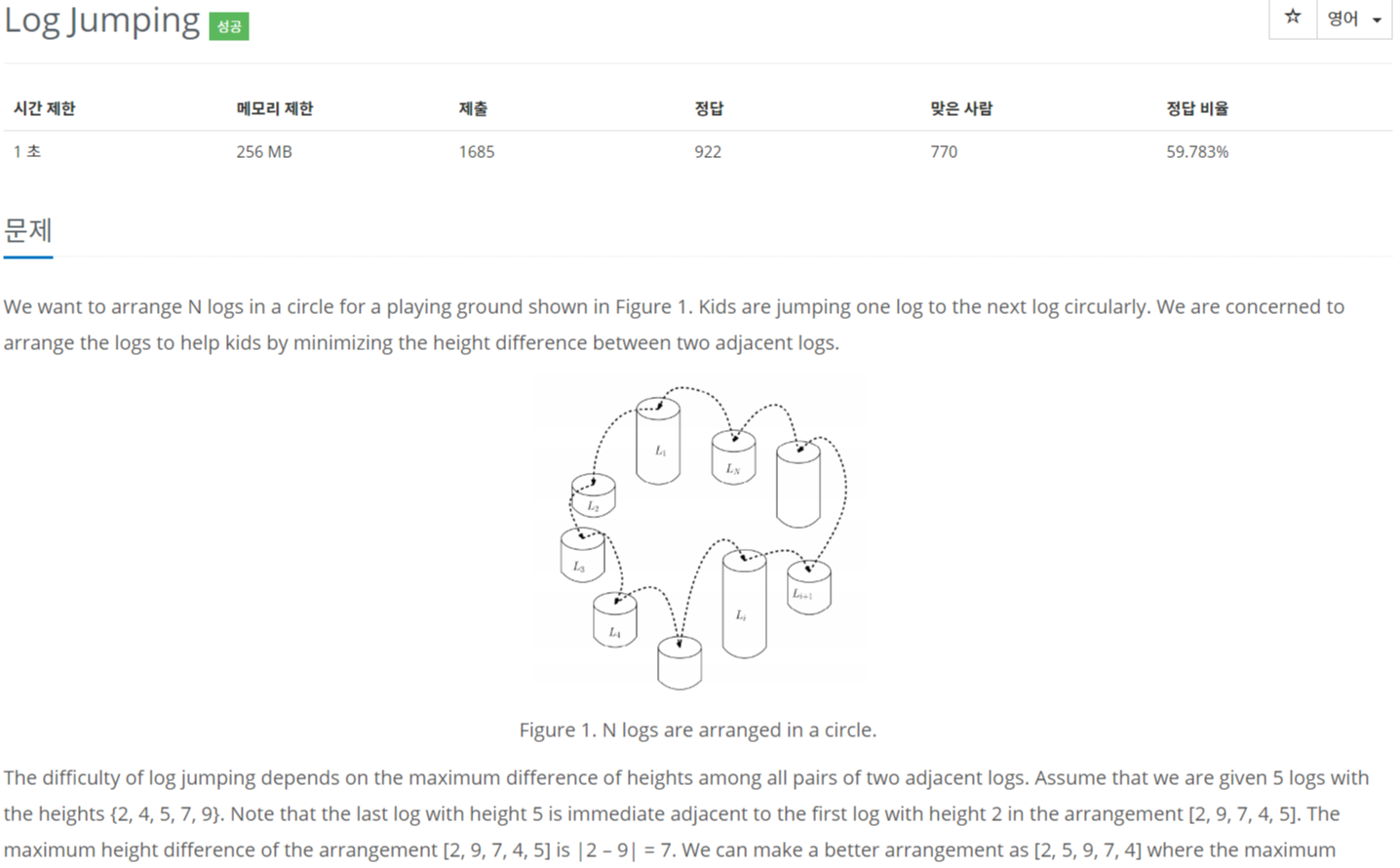
N개의 통나무의 높이가 주어지고 우리는 이 통나무를 동그랗게 배치할 것이다.
이때, 통나무 사이의 높이 차이 중 가장 큰 값이 가장 작게 나올 때, 그 값을 출력하는 알고리즘을 구현하라.
예를 들어, 높이가 2,4,5,7,9 인 5개의 통나무를 가지고 [ 2 - 4 - 5 - 7 - 9 ]로 배치를 하면,
통나무 높이 차이 중 가장 큰 값은, 높이가 2인 통나무와 9인 통나무 사이의 높이 차인 7이 된다.
배치를 바꿔 [7 - 4 - 2 - 5 - 9 ] 로 배치를 하면, 통나무 높이 차이 중 가장 큰 값은 높이가 5인 통나무와 9인 통나무 사이의 높이 차인 4가 된다.
[알고리즘설계]
1. 통나무 높이가 주어지면 오름차순으로 sort를 진행한다.
2. n개의 통나무가 주어졌을 때, 높이가 작은 통나무부터 A1, A2, ⋯ , An 이라고 하자.
우리는 높이 차이를 최소화해야 하므로, 비슷한 통나무들끼리 배치해줘야 한다.
따라서 가장 작은 통나무부 A1을 배치하고, 그다음에는 A2, A1, A3 식으로 주변에 배치를 진행할 것이다.
-> ⋯ A4, A2, A1, A3, A5 ⋯ 형태로 배치한다.
3. 실제로 배치할 필요는 없으므로, 2번의 아이디어를 통해 A1부터 시작해 양 옆에 올 통나무들과의 거리 차를 계속 계산해나가며, 그중 MAX를 저장한다.
#include<iostream>
#include<algorithm>
using namespace std;
int list[10000];
int main(void) {
int test_Case;
cin >> test_Case;
for (int i = 0; i < test_Case; i++) {
int ninput;
cin >> ninput;
for (int j = 0; j < ninput; j++)
cin >> list[j];
sort(list, list + ninput);
int distance = list[2] - list[0];
if (ninput % 2 == 1) {
for (int j = 1; j <= ninput - 4; j += 2) {
if (list[j + 2] - list[j] > distance)
distance = list[j + 2] - list[j];
if (list[j + 3] - list[j + 1] > distance)
distance = list[j + 3] - list[j + 1];
}
}
else {
for (int j = 1; j <= ninput - 5; j += 2) {
if (list[j + 2] - list[j] > distance)
distance = list[j + 2] - list[j];
if (list[j + 3] - list[j + 1] > distance)
distance = list[j + 3] - list[j + 1];
}
if (list[ninput - 1] - list[ninput - 3] > distance)
distance = list[ninput - 1] - list[ninput - 3];
}
if (i != test_Case - 1)
cout << distance << "\n";
else
cout << distance;
}
}Indexing이 까다로워서 실수가 있었지만, 그래도 ACM-ICPC 문제 치고는 쉬운 편인 것 같습니다.
'Problem Solving > ICPC' 카테고리의 다른 글
| [ACM-ICPC][BOJ] 11501 - Stock 문제풀이 (0) | 2019.07.24 |
|---|---|
| [ACM-ICPC][BOJ] 13560 - Football Game 문제풀이 (0) | 2019.07.24 |
| [ACM-ICPC][BOJ] 11502 - 3Primes Problem 문제풀이 (0) | 2019.07.23 |
| [ACM-ICPC][BOJ] 13567 - ROBOT 문제풀이 (0) | 2019.07.21 |
| [ACM-ICPC][BOJ] 13565 - Percolation 문제풀이 (0) | 2019.07.21 |