안녕하세요, 여행벌입니다.
오늘은 문자열 탐색에 특화된 자료구조 트라이(Trie)에 대해서 포스팅해보겠습니다.
트라이 Trie 기본 개념
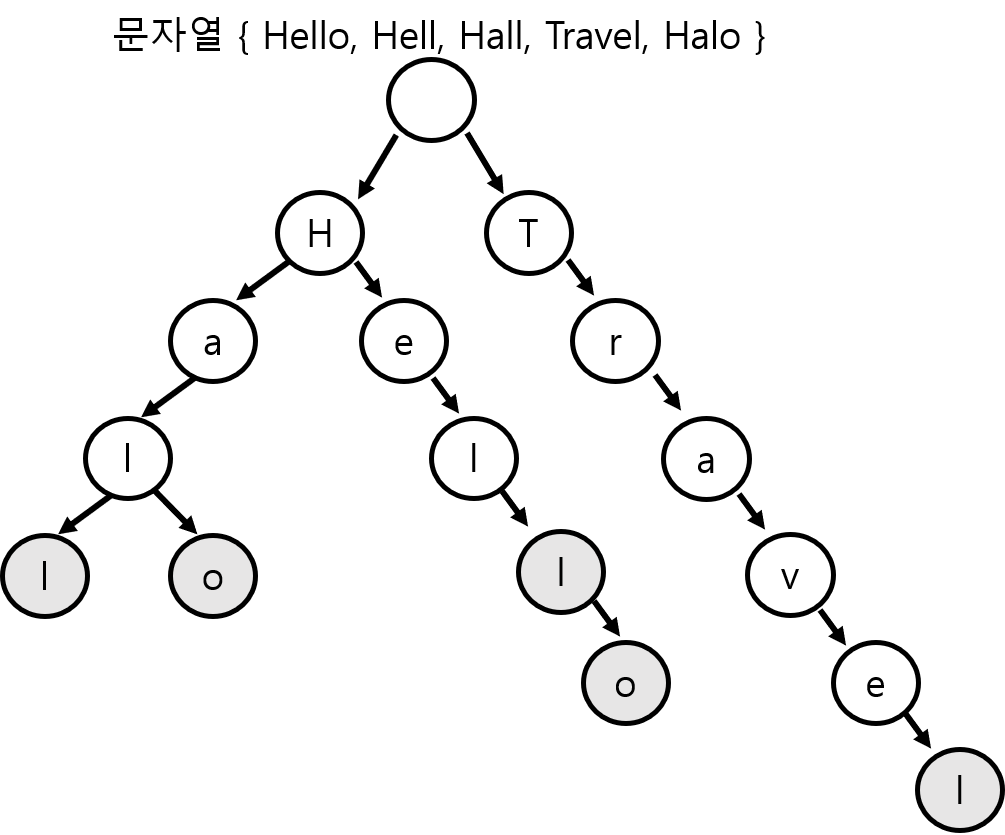
● 트라이는 문자열의 집합을 표현하는 트리 자료 구조로 위의 그림과 같은 형태로 이루어져 있습니다. 트라이의 한 노드를 표현하는 객체는 자손 노드들을 가리키는 포인터 목록과, 이 노드가 종료 노드인지를 나타내는 불린 값 변수로 구성됩니다.
● 자손 노드들을 가리키는 포인터 목록은 입력에 등장할 수 있는 모든 문자에 각각 대응되는 원소를 갖는 고정 길이 배열로 구현합니다.
● 루트에서 한 노드까지 내려가는 경로에서 만나는 글자들을 모으면 해당 노드에 대응되는 접두사를 얻을 수 있습니다. 따라서, 각 노드에 대응되는 문자열을 따로 저장할 필요가 없습니다. 즉, Hello, Hell 은 겹치는 부분(Hell) 을 따로 저장해두는 것이 아니라 하나의 경로에 같이 저장하는 것을 확인할 수 있습니다.
● 문자열은 정수, 실수형 변수와 다르게 비교하는 데 최악의 경우 문자열의 길이에 비례하는 시간이 걸립니다. 따라서, 정수나 실수 키에 대해서는 잘 동작하는 탐색 자료 구조들도 문자열을 키로 사용할 때는 시간이 오래 걸릴 수 있습니다. 예를 들어, N개의 원소를 갖는 이진 검색 트리에서 원하는 원소를 찾으려면 O(logN)번의 비교를 해야 하지만, 문자열의 비교에서는 최대 문자열의 길이를 M이라고 하면 O(MlogN)이 최종 시간 복잡도가 됩니다. 이런 문제를 해결하기 위해 자료구조 트라이(Trie)가 등장했습니다.
● 즉, 트라이 자료구조를 이용하면 집합 내에서 문자열 원소를 찾는 작업을 O(M) 시간만에 할 수 있습니다.
트라이 Trie 코드 구현 (C++)
트라이 객체는 포인터와 마지막 노드인지 아닌지 체크를 해주는 bool 변수로 이루어져 있다고 위에서 언급했습니다. 입력되는 문자열이 알파벳 대문자인 경우의 트라이 객체를 구현해보겠습니다.
struct Trie {
bool finish; //끝나는 지점을 표시해줌
Trie* nextNode[26]; //26가지 알파벳에 대한 트라이 포인터 배열
Trie() {
finish = false;
memset(nextNode, 0, sizeof(nextNode));
}
~Trie() {
for (int i = 0; i < 26; i++)
if (nextNode[i])
delete nextNode[i];
}
void insert(const char* key) {
if (*key == '\0')
finish = true; //문자열이 끝나는 지점일 경우 표시
else {
int next = *key - 'A';
if (nextNode[next] == NULL)
nextNode[next] = new Trie(); //탐색이 처음되는 지점일 경우 동적할당
nextNode[next]->insert(key + 1); //다음 문자 삽입
}
return;
}
Trie* find(const char* key) {
if (*key == 0)
return this;
int next = *key - 'A';
if (nextNode[next] == NULL) // 문자열에 없음.
return NULL;
return nextNode[next]->find(key + 1); // 다음 문자로 탐색을 진행
}
};트라이 Trie 복잡도 계산
트라이에서 중요한 연산은 find 함수와 insert 함수입니다. 이 함수들은 문자열의 길이만큼 재귀 호출을 수행하기 때문에, 두 함수의 시간 복잡도는 모두 문자열의 길이(M)에 비례합니다. 즉, 트라이에 포함된 다른 문자열의 개수(N)과는 상관이 없다는 것을 알 수 있습니다. 따라서 트라이는 빠른 속도가 필요한 검색 엔진이나 기타 문자열 처리 프로그램에서 자주 사용됩니다.
● insert 함수 시간 복잡도 : O(M)
● find 함수 시간 복잡도 : O(M)
트라이 Trie 단점
트라이 자료구조는 치명적인 단점이 있습니다. 바로, 필요로 하는 공간(메모리)이 너무 크다는 문제입니다. 그 이유는 포인터 배열 때문입니다. 알파벳 대문자만 저장한다고 해도 트라이의 각 노드는 26개의 포인터를 저장해야 합니다. 또, 입력되는 문자열들이 접두사를 전혀 공유하지 않는 최악의 경우 트라이에는 입력되는 문자열들의 전체 길이만큼의 노드가 필요합니다.
트라이 꿀팁 Tip
위의 단점 때문에 트라이를 사용해야 하는 알고리즘 문제에서는 대체로 입력되는 문자열들의 전체 길이를 알려줍니다! 문자열을 탐색하는 문제 + 입력되는 문자열들의 전체 길이를 알려주는 힌트가 문제에 있다면, 트라이 자료구조를 사용하는 문제인지 아닌지 의심해볼 수 있습니다.
트라이 예시
#include<iostream>
#include<string>
#include<vector>
#include<cstring>
#include<algorithm>
using namespace std;
struct Trie {
bool finish; //끝나는 지점을 표시해줌
Trie* nextNode[26]; //26가지 알파벳에 대한 트라이 포인터 배열
Trie() {
finish = false;
memset(nextNode, 0, sizeof(nextNode));
}
~Trie() {
for (int i = 0; i < 26; i++)
if (nextNode[i])
delete nextNode[i];
}
void insert(const char* key) {
if (*key == '\0')
finish = true; //문자열이 끝나는 지점일 경우 표시
else {
int next = *key - 'A';
if (nextNode[next] == NULL)
nextNode[next] = new Trie(); //탐색이 처음되는 지점일 경우 동적할당
nextNode[next]->insert(key + 1); //다음 문자 삽입
}
return;
}
Trie* find(const char* key) {
if (*key == 0)
return this;
int next = *key - 'A';
if (nextNode[next] == NULL) // 문자열에 없음.
return NULL;
return nextNode[next]->find(key + 1); // 다음 문자로 탐색을 진행
}
};
int main(void) {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
Trie* trie = new Trie();
trie->insert("HELLO");
trie->insert("HELL");
trie->insert("HALL");
trie->insert("HALO");
trie->insert("TRAVEL");
cout << trie->find("HELLO") << endl;
cout << trie->find("HALO") << endl;
cout << trie->find("TRAVELBEEEE") << endl;
cout << trie->find("BEE") << endl;
delete trie;
}
대문자로 이루어진 문자열 { "HELLO", "HELL", "HALL", "HALO", "TRAVEL" } 을 Trie에 삽입하고 "HELLO", "HALO", "TRAVELBEEEE", "BEE" 를 탐색해보겠습니다. 결과는 다음과 같습니다.
010AEFC0
010AF220
00000000
00000000"TRAVELBEEEE", "BEE" 는 Trie에 존재하지않으므로, null 값이 반환된 것을 확인할 수 있습니다.
이상으로 문자열 탐색에 특화된 자료구조 트라이(Trie) 포스팅을 마치겠습니다.
'Computer Science > Algorithm' 카테고리의 다른 글
| [알고리즘] KMP : 문자열 검색 알고리즘 (0) | 2020.05.08 |
|---|---|
| [알고리즘] 최단 경로 알고리즘 - 다익스트라(Dijkstra) (0) | 2020.04.29 |
| [알고리즘] 깊이 우선 탐색(DFS)이란 (0) | 2020.04.06 |
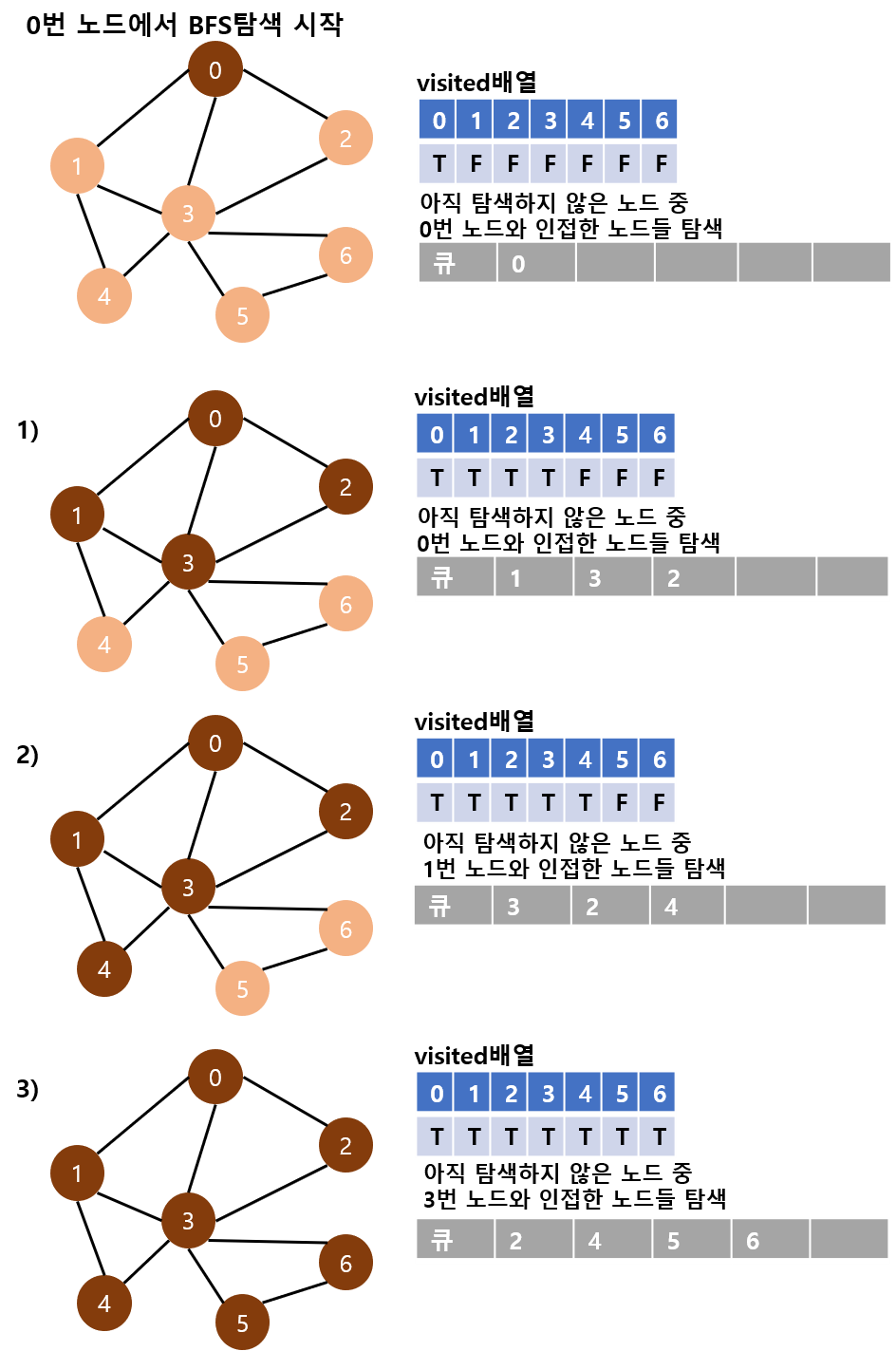
| [알고리즘] 너비 우선 탐색(BFS) 이란 (0) | 2020.04.03 |
| [알고리즘] 서로소 집합(Disjoint set) & 유니온-파인드 (Union-Find) 란 (1) | 2020.04.01 |