문제 : https://www.acmicpc.net/problem/2463
[ 알고리즘풀이 ]
문제 예시를 통해 자세히 뜯어보겠습니다.

다음과 같은 상황에서 u < v 인 모든 두 정점 u, v 에 대한 Cost(u, v) 의 총합은 다음과 같습니다.
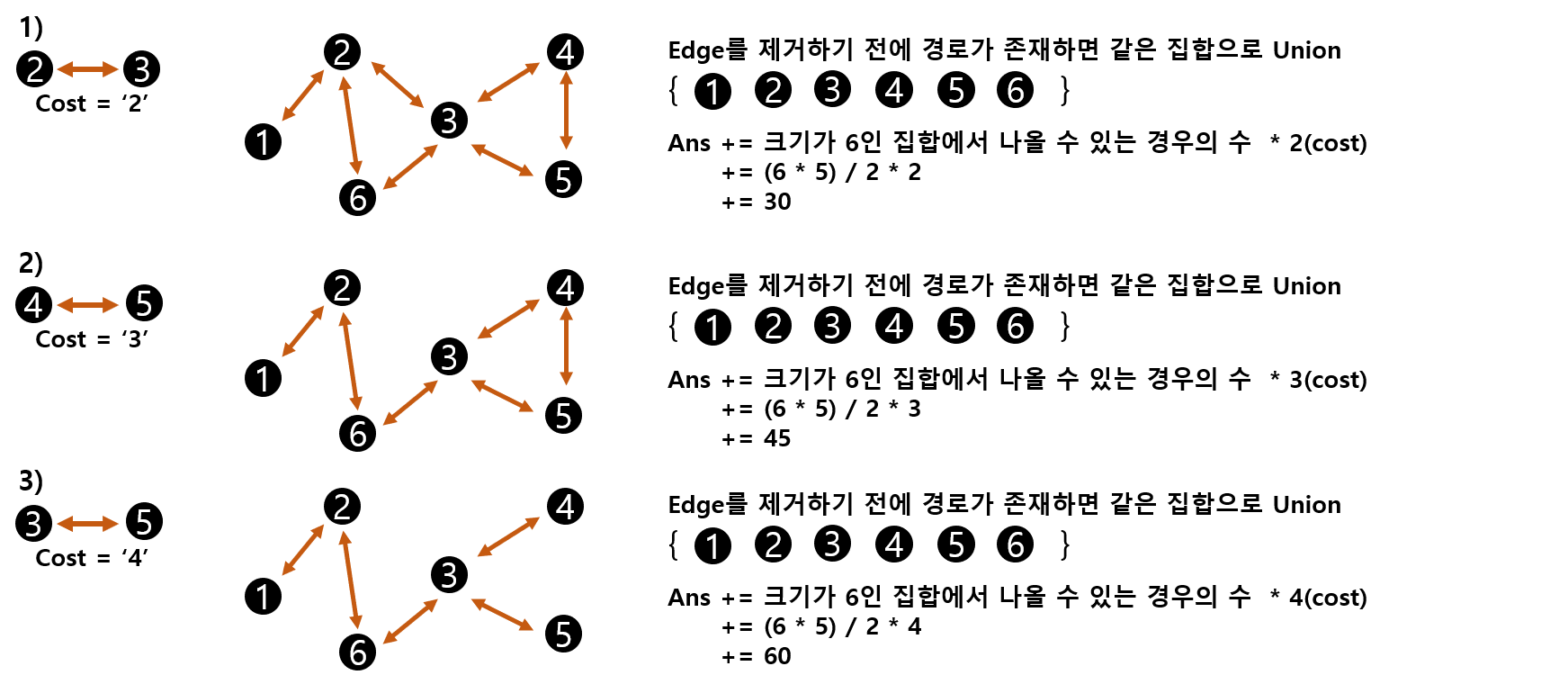

→ 간선을 제거했을 때, 경로가 끊기는지가 중요!
하지만, 이렇게 답을 구하려면 M개의 간선을 하나씩 제거하며, 매번 Union-Find 기법으로 N개의 정점에 대해서 Grouping 을 해줘야되므로 O(N * M) 복잡도를 가진다. 따라서, 제한 시간 안에 문제를 해결할 수 없다.
시간 제한 안에 문제를 해결하려면 관점을 전환해야됩니다. Cost가 작은 간선을 하나씩 제거하는 것이 아니라, Cost가 가장 큰 간선부터 하나씩 간선을 추가한다고 생각을 하면 간선을 하나 추가하고, 그 두 정점만 Union-Find 기법으로 Grouping 해주면 되므로 시간 복잡도를 줄일 수 있습니다.
→ 간선을 추가했을 때, 경로가 생기는지 보자!



#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
using namespace std;
const int MOD = 1000000000;
int N, M, x, y, cost;
int root[100001], setSize[100001];
priority_queue<pair<int, pair<int, int>>> edge;
int find(int num) {
if (num == root[num])
return num;
return root[num] = find(root[num]);
}
void merge(int num1, int num2) {
root[num2] = num1;
setSize[num1] += setSize[num2];
setSize[num2] = 1;
return;
}
int main(void) {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> N >> M;
for (int i = 0; i <= N; i++) {
root[i] = i;
setSize[i] = 1;
}
long long total = 0;
for (int i = 0; i < M; i++) {
cin >> x >> y >> cost;
edge.push({ cost,{x,y} });
total += cost;
}
long long result = 0;
for (int i = 0; i < M ; i++){
pair<int, pair<int, int>> temp = edge.top();
edge.pop();
int pNum1 = find(temp.second.first);
int pNum2 = find(temp.second.second);
int curCost = temp.first;
//둘이 같은 집합이 아닌 경우
if (pNum1 != pNum2){
result += (((1L * setSize[pNum1] * setSize[pNum2]) % MOD) * total) % MOD;
result %= MOD;
//같은 집합으로 합친다
merge(pNum1, pNum2);
}
total -= curCost;
}
cout << result << '\n';
return 0;
}
'Problem Solving > BOJ' 카테고리의 다른 글
| [BOJ] 11085 : Protest - travelbeeee (0) | 2020.03.30 |
|---|---|
| [BOJ] 14868 : 문명 - travelbeeee (0) | 2020.03.27 |
| [BOJ] 7579 : 앱 - travelbeeee (0) | 2020.03.23 |
| [BOJ] 1351 : 무한 수열 - travelbeeee (0) | 2020.03.20 |
| [BOJ] 1167 : 트리의 지름 - travelbeeee (0) | 2020.03.20 |